Publications
My research interests are graph representation learning and geometric deep learning. Currently, I am working on graph diffusion models, where I am interested in understanding the failure modes of discrete diffusion applied to graph generation, how symmetry constraints and equivariant architectures influence their learning dynamics, and how we can scale up to large graph generation.
During my Master’s, I investigated the generalization behavior of graph neural networks, proposing approaches to mitigate structural limitations such as over-squashing and over-smoothing. I also introduced the first framework demonstrating that GNNs can memorize node labels.
In my Bachelor’s, I primarily worked on deep learning for computer vision problems. Below you will find a list of my most representative publications.
Your Discrete Graph Diffusion Model is Secretly Memorizing.
BeNTo: Beyond Next Token Prediction, NeurIPS Workshop. (2026)
Empirical evidence shows you can train a graph diffusion model on just one graph and still generalize without memorizing the training graph. Existing works on equivariant denoisers suggests GDMs cannot copy their training graphs exactly owing to permutation symmmetries and sample-level metrics suggest generalization. But what if your GDM is secretly memorizing the training graph?
When Edge-Independence Fails: Joint Diffusion with Latent Sociability Priors.
NeurIPS (2026)
Discrete graph diffusion models corrupt the graph structure through a Markovian noise model, combined with the exchangeability requirement the terminal distribution is an E-R graph. We show that any GNN denoiser applied to an E-R graph approximately outputs an E-R graph, making effective denoising difficult. We address the root cause by introducing the Latent Sociability Prior (LSP) and a joint diffusion process that co-evolves latent node sociability variables and graph structure, removing edge independence while preserving exchangeability.
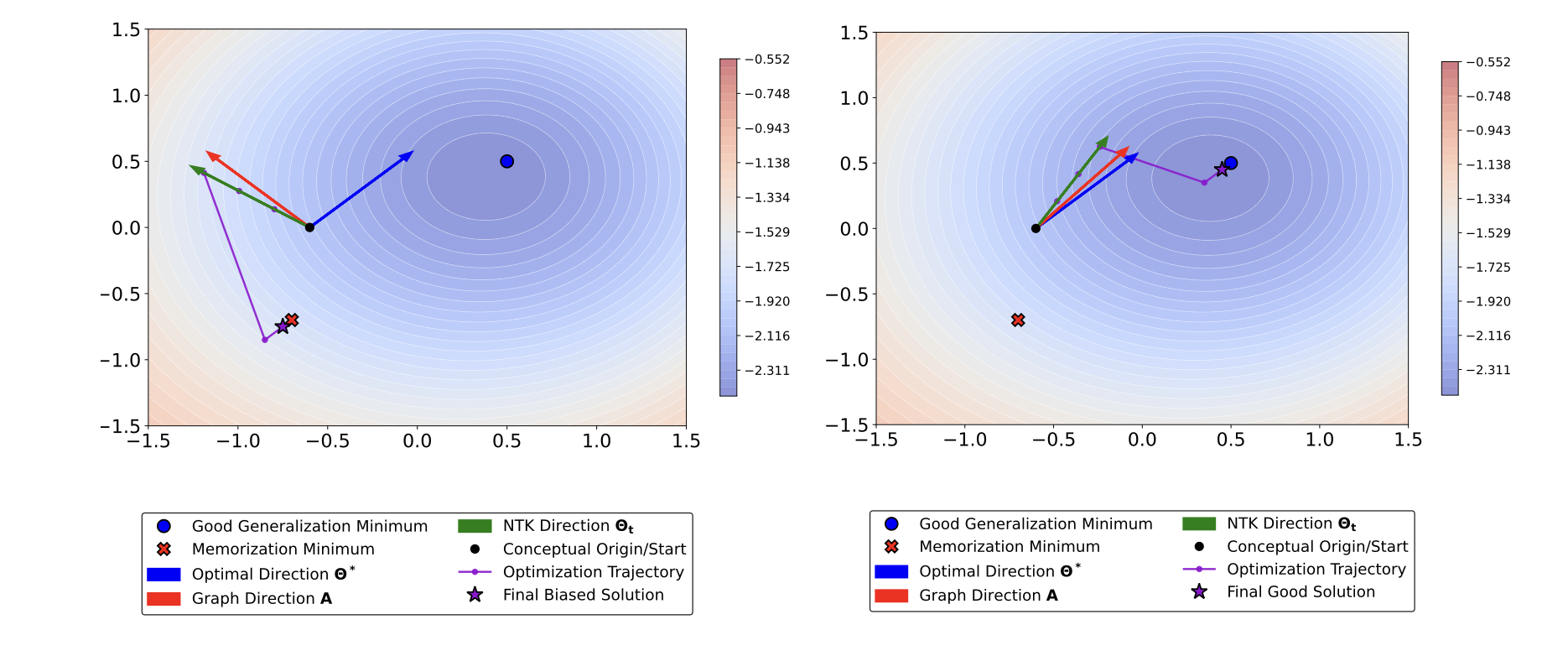
Memorization in Graph Neural Networks.
NeurIPS (2025)
Do GNNs also memorize their training data? Why are only certain nodes memorized? How do you explain the emergence of memorization in GNNs? How to mitigate memorization in GNNs? We propose the first framework to analyze memorization in node classification. We find novel connections to graph homophily, implicit bias of GNNs and a novel metric to find nodes highly susceptible to memorization.
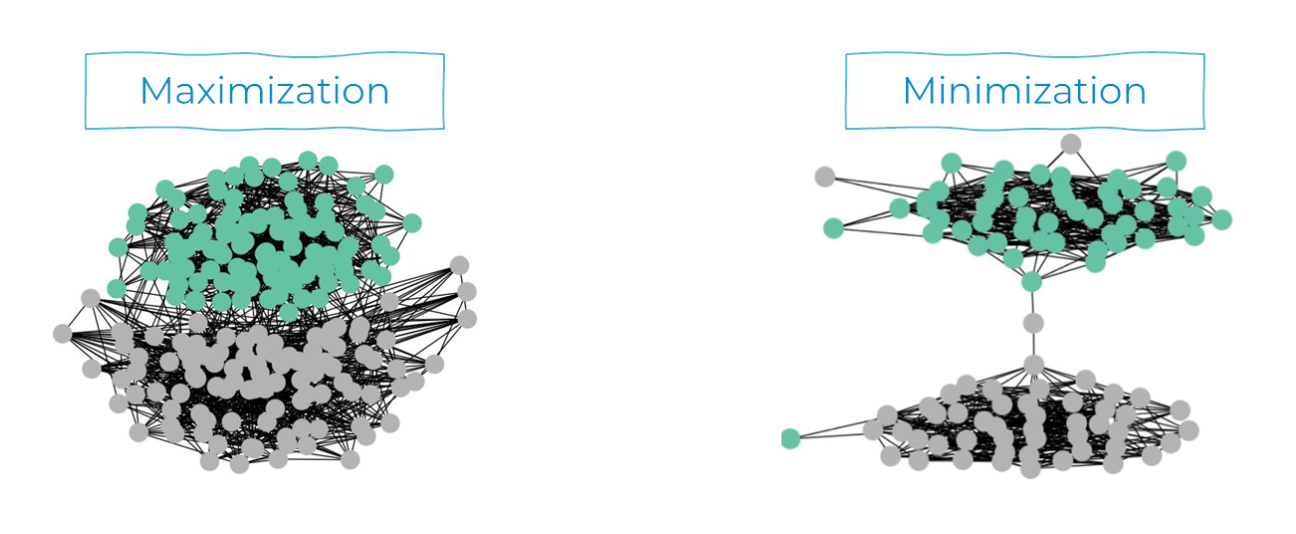
GNNs Getting ComFy: Community and Feature Similarity Guided Rewiring.
ICLR (2025) *Equal contributions
Graph rewiring methods have emerged as a powerful technique to address over-squashing and over-smoothing in Graph Neural Networks (GNNs). However, the underlying mechanisms that drive their effectiveness remain poorly understood. In this work, we investigate why spectral gap maximization works as a rewiring objective and under what conditions it may fail. We show that maximizing the spectral gap is not always beneficial and introduce a novel framework that leverages both community structure and feature similarity to guide graph rewiring.
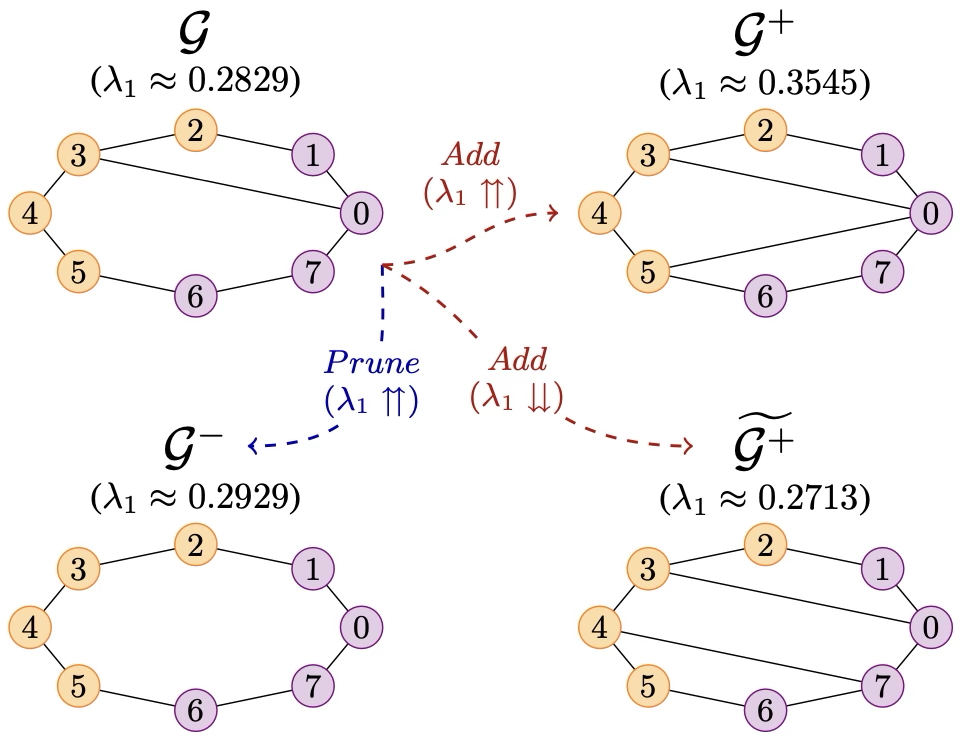
Spectral Pruning Against Over-Squashing and Over-Smoothing.
NeurIPS (2024) *Equal contributions
We introduce the Braess Paradox in the context of Graph Neural Networks for the first time, showing that adding edges that maximize spectral gap can actually hurt performance. Building on this insight, we propose a novel spectral graph pruning strategy that simultaneously addresses over-squashing and over-smoothing. Our method not only improves GNN performance but also discovers graph lottery tickets - sparse subgraphs that maintain or exceed the performance of the full graph.
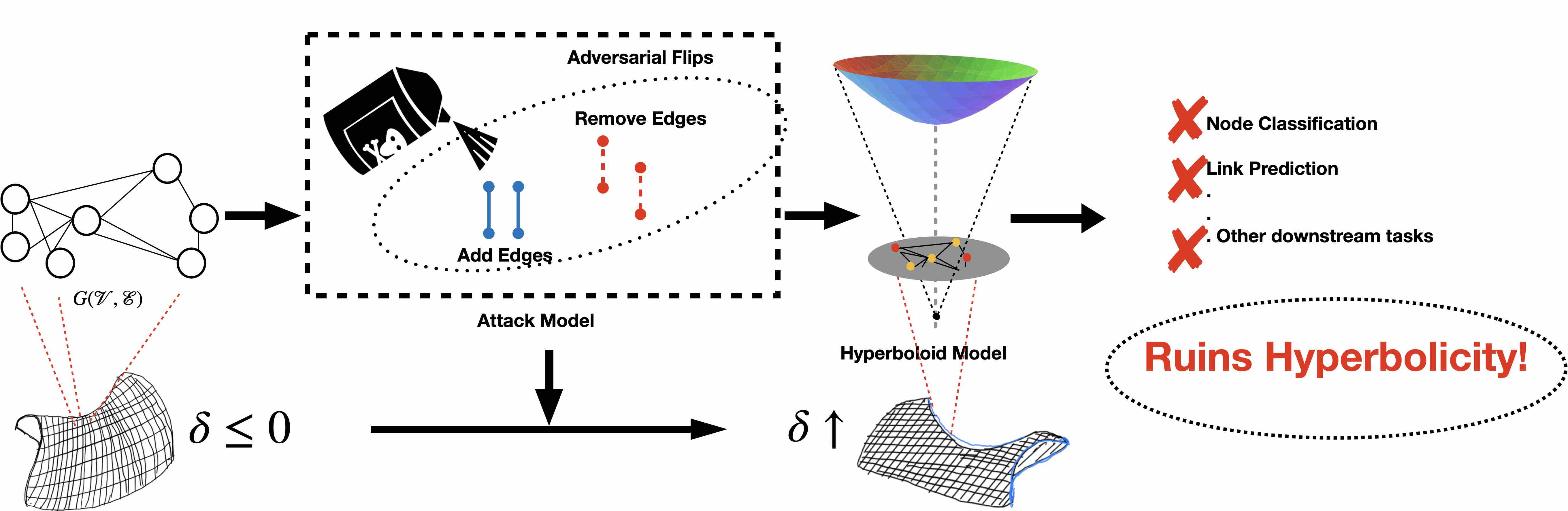
Graph of Thrones: Adversarial Perturbations dismantle Aristocracy in Graphs.
AAAI Student Poster (2021)
We investigate how adversarial perturbations affect graph hyperbolicity.
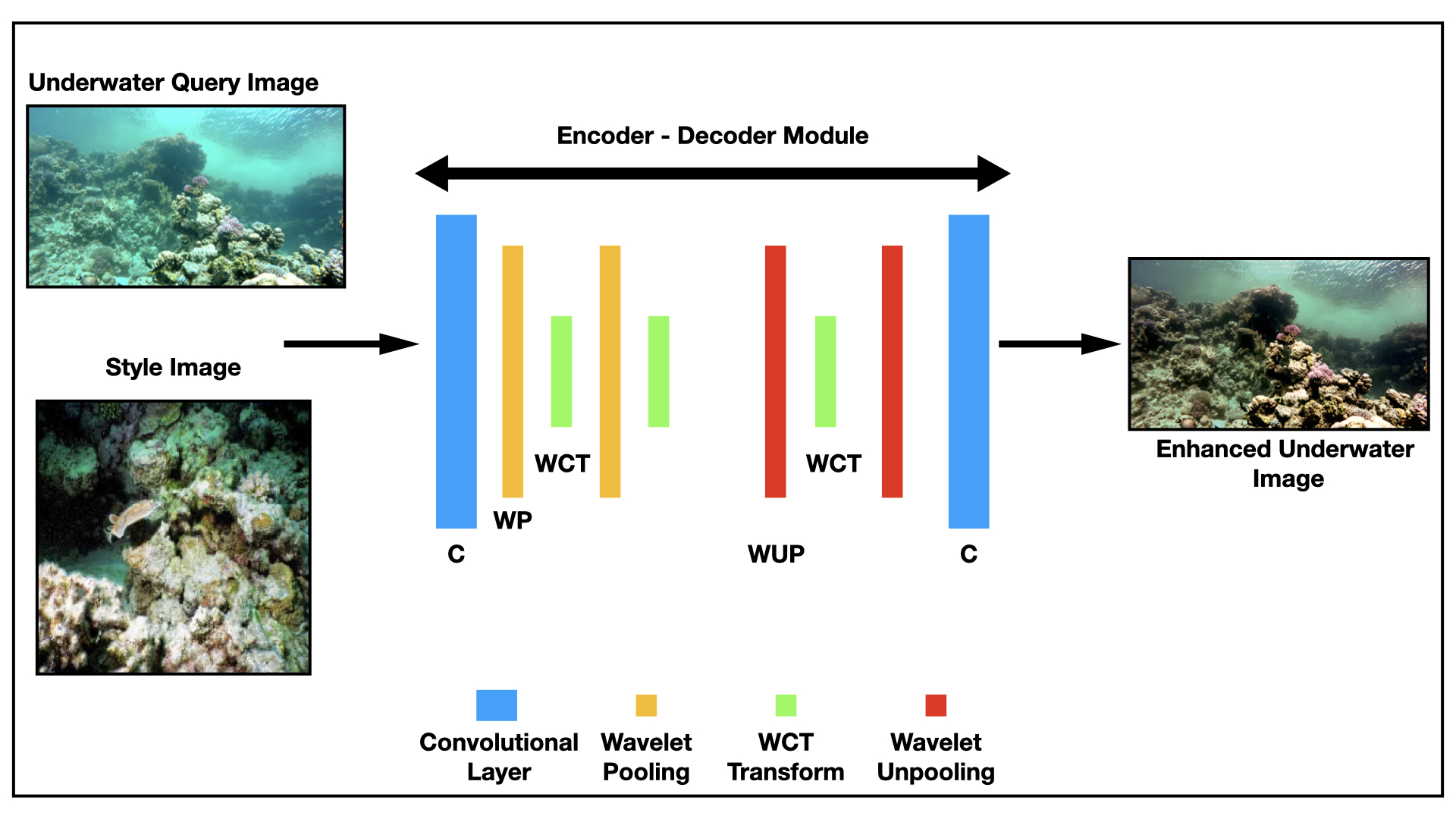
Exemplar-based Underwater Image Enhancement Augmented by Wavelet Corrected Transforms.
CVPR Workshop (2019)
We propose a novel deep learning framework for underwater image enhancement using wavelet-corrected transformations.
PredGAN: A Deep Multi-Scale Video Prediction Framework for Detecting Anomalies in Videos.
ICVGIP (2018)
We propose a multi-scale video prediction framework with adversarial training for detecting anomalies in videos.